
ここでは数に関するちょっとした疑問や質問を通して頭を使っていただくコーナーとして設けました。
気が付いた時点で少しづつ問題を加えていく予定ですので、時々、このコーナーにお立ち寄りください。
1は0.99999999・・・・?
n=0.9999999・・・・・・・と無限に9がつながる少数とします。
この少数を10倍すると
10n=9.9999999・・・・・・・
となります。これから10n-nを求めます。
とすると
10n-n=9.9999999・・・・・・・ー0.9999999・・・・・・・
ですから
9n=9
n=1
となります。
n=0.9999999・・・・・・・がどうしてn=1となってしまうのでしょうか?
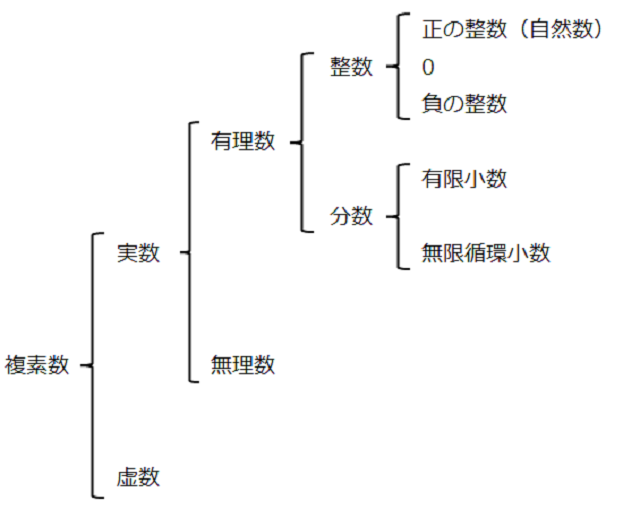
【数の分類】
小中学校で扱う数は有理数です。この内、分数は有限小数と無限循環小数に分けられますが、有限小数は分数を少数で表したときに割り切れる数、無限循環小数は分数を少数で表したときに割り切れないでパターンが巡回して現れる数のことを言います。
例えば2/5=0.4と割り切れるから有限小数、1/3=0.333333・・・は3の数字が無限につながるので無限循環小数といいます。そして繰り返される数字 3 を循環節といいます。
1/7=0.142857142857142857…は142857が循環節となる無限循環小数となります。
無理数とは循環しない無限小数となります。
例えば円周率π=3.14159265358979…は循環しない無限小数となるため、無理数といいます。
【円周率の覚え方】
円周率を求める方法は様々な方法がありますが、小中学生でもわかる方法は実験的に求める方法です。
円周率=円周の長さ÷直径の長さ ですから、何か丸いものを用意して計測すれば求めることができます。
例えば、缶詰の直径とその周囲の長さを求めます。周囲の長さは糸などで巻いて、その糸の長さを調べれば求めることができます。
求めた缶詰の周囲の長さを缶詰の直径の長さで割れば、おおよその円周率の値が求まります。
さて正しい円周率はどのように覚えたらよいのでしょうか?
3.141592653589793238462643383279・・・とつながりますが、これを語呂合わせで
産医師異国に向かい産後薬なく産婦みやしろに虫散々闇に鳴く(さんいしいこくにむかいさんごやくなくさんぷみやしろにむしさざんやみになく)と覚えれば少数30桁まで言うことができます。
【循環する無限小数は分数になる】
例えば
y=0.424242…と42が循環節となっている無限小数とすれば
100×y=42.424242…となり、
100×y-y=42.424242-0.424242であるから
99y=42
y=42/99 約分して y=14/33 となります。
【1=0.9999999… はどう考えたらよいの?】

x=1/3はx=0.3333…の無限小数になります。
このときx=0.3333を3倍したとき 3x=0.9999…となります。
そのため0.9999…が1でない場合
0.3333…も1/3にすることができません。
従って、0.9999…=1となります。
しかし、何か納得できませんね。0.9999…は概ね1なのではなく、0.9999・・・=1なのです。
もし、0.9999…≠1でないならば、
0.9999<A<1 となるAが存在するはずです。しかし、その存在を見つけることができないから、
0.9999=1である という証明もあります。
また、
0.1111… =1/9
0.2222… =2/9
0.3333… =3/9=1/3
0.4444… =4/9
0.5555… =5/9
0.6666… =6/9=2/3
0.7777… =7/9
0.8888… =8/9
となります。同じように続けると
0.9999… =9/9=1
となります。という証明も見られました。
いずれにしても0.9999…と1の間に差があることを指摘できないのであるから、同一の数値(数字ではない)と考える ということでしょうか?
3個のパンを5人で分けるのに、切る回数が最も少ない切り方は?

ここに3つの全く同じパンがあります。このパンを5人に分けるのに、最も切る回数を少なくして分けるにはどうしたらよいでしょうか?
単純に考えれば、それぞれのパンを5等分し、各自が3つずつもらうですよね。これだと1つのパンを5等分するのに4回切らなくてはならないので全部で12回切ることになります。
では、まず、3つのパンを全て半分にし、それぞれがその半分のパンを取ります。残った1つの半分のパンを5等分すれば均等になります。この分け方だと、半分に切るのに3回、1つの半分のパンを5等分するのに4回切ればよいことになります。
これで合計7回で済むことになりますね。